RL 스터디 개념 정리(1) 1~2강 RL 용어 정리 및 MDP

https://www.youtube.com/watch?v=2pWv7GOvuf0&list=PLzuuYNsE1EZAXYR4FJ75jcJseBmo4KQ9-

스터디 시작 전 David Silver 교수님의 강의를 듣고 개념 정리를 했습니다.

 

 

 

Introduction to Reinforcement Learning

• 문제 setting, 용어 등 기본적인 소개

강화학습에서는 오로지 보상에만 초점을 맞춘다. 미리 정해진 정답값을제공하는 기존 ML과 달리, 강화학습은 reward를 보고 가장 최적의 솔루션을 찾아내는 데 중점을 둔다.

즉, 강화학습의 목적은 최대 보상을 얻기 위해 특정 행동을 지시하는 것이 아니라, RL이 받고 있는 보상을 최적화 하는 방법을 알아내는 것이다. 이런 접근 방식은 인간은 결국 sub-optimal한 정답값에 도달하게된다는 생각에서 출발한다. 따라서 복잡한 시나리오에서 사람이 답을 알려주며 학습을 하게 되면 결국 sub-optimal한 정답값을 학습하게 되기 때문에 차선책에 만족하는 경우가 많다. 강화학습은 알고리즘이 보상을 기반으로 자유롭게 탐색하고 최적화 하도록 함으로써 복잡한 시나리오에서 자율적으로 global optimal을 찾아나갈 수 있다.

 

핵심적인 차이점은 강화학습은 순서가 중요한 sequential data를 사용한다는 점이다. 고정된 예시가 아니라 경험을 통해 학습함으로써, 시간이 지남에 따라 행동에 대한 보상이 누적되며 agent가 따르는 policy가 형성된다.

 

RangL: A Reinforcement Learning Competition Platform

 

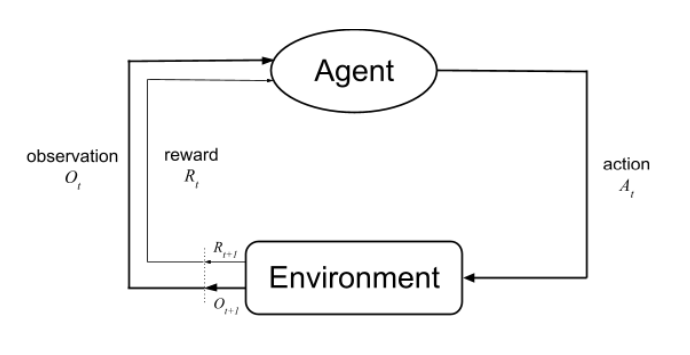
강화학습의 목표는 누적된 총 Reward를 최대화하는 것이다.

• Reward: 단일 스칼라 숫자값, 시간 t 동안 agent가 얼마나 잘 수행했는지 나타내는 지표
• Agent: Reward의 축적된 합을 최대화하는 것이 목적인 것
  • 강화학습을 수행하기 위해 Reward를 단일 숫자 값으로 표현할 수 있어야 하며, reward가 스칼라 값 하나로 치환 불가능할 정도로 복잡한 경우는 강화학습이 적합하지 않을 수 있다.

Agent는 다음 Action을 결정하는 데 State를 기반으로 의사 결정을 내린다.

• State: 다음에 무슨 행동을 할지 결정하기 위한 모든 정보들
  • Environment State: environment가 observation(행동에 따라 상황이 어떻게 바뀌었는지)과 reward를 계산할 때 쓴 모든 정보(Agent는 알 수 없는 정보) = Markov
  • Agent State: 다음 action을 하기 위해 필요한 모든 정보 (reward와 observation 값/가공값)
  • Markov State: 어떤 tate가 Markov한지/아닌지
    • Markov하다 = 미래는 전체 히스토리가 아닌 현재 상태에만 의존한다. t 시간에 대한 결정을 할 때 바로 이전 (t-1)에만 의존하여 결정하는 것, 즉 (t+1) 미래의 시간은 현재 t와 관련 있으며, 과거 (t-1)와 그 이전의 시간들과는 관련 없다. 문제를 단순화 하여 agent가 이전의 모든 상태를 기억하지 않고도 그 순간의 보상을 극대화하는 데 집중할 수 있다.

 

 

Agent의 구성 요소

 

Agent의 목표는 Value Function을 최대화 하는 것이다. 이를 위해서는 장기적으로 가장 높은 Reward를 가져오는 최선의 Action을 선택하도록 Policy를 최적화해야 한다. Value Function과 Policy는 상호 의존적이며 반복적으로 개선된다.

• Policy: State를 Action에 매핑하는 Agent의 행동
  • Deterministic Policy: State가 주어지면 결정적으로 action이 리턴
  • Stochastic Policy: State가 주어지면 가능한 여러 action들이 일어날 확률이 리턴

• Value Function: 현재 Policy에 따라 State가 얼마나 좋은지 나타내는 지표, 종료될 때까지 받을 수 있는 미래 리워드의 합산
  • v_π(s): State=s에서 시작했을 때, 정의된 policy에 따라 받게되는 총 기댓값 
  • r: discount factor = 미래의 리워드는 불확실하니까 등의 이유로

• Model: Model을 활용하여 Environment가 어떻게 될지 예측할 수 있다
  • State s에서 Action a를 했을 때
    • State=s에서 Action=a를 취한 후 즉각적인 reward는 무엇을 받을지 예측
    • State=s에서 Action=a를 취함으로써 발생할 다음 State가 무엇이 될지 예측
  • 이러한 모델링 기법은 RL에서 사용될 수도(model-based) / 사용되지 않을수도(model-gree) 있다.

 

 

RL의 분류 (value-based/policy-based/actor critic) vs (model-free/model-based)

 

강화학습 방법은 두 가지로 분류할 수 있다.

• value-based vs policy-based vs actor critic
  • value-based: policy(x), value function(o) -> 각 state에서 value를 학습하여, 이로부터 도출된 정책을 따르는 데 의존
    • value function만 있더라도 agent 역할을 할 수 있는 경우
  • policy-based: policy(o), value function(x) -> value function을 하용하지 않고 policy를 직접 최적화하는 데 중점
  • actor critic: policy(o), value function(o) -> policy와 value function을 동시에 학습
• model-free vs model-based
  • model-free: policy and/or value function(o), model(x)
    • 모델을 내부적으로 만들지 않고
  • model-based: policy and/or value function(o), model(o)
    • agent가 내부적으로 environment 모델을 추측하여 만들어서, model에 근거한 action이 이루어짐

 

RL 문제의 종류

 

강화학습에서 Agent는 크게 두 가지 방법으로 Policy를 개선할 수 있다.

• Learning: Agent가 environment를 알지 못할 때, environment와 상호작용하면서 policy를 개선해나가는 것
• Planning: Agent가 environment(reward & state transition)를 알고 있을 때, 실제로 environment에서 동작하지 않고도 내부 계산만으로 다양한 시나리오를 시뮬레이션하고 평가함으로써 policy를 개선해나간다
  • ex. 알파고의 몬테카를로 Search

Agent의 주요 목표는 크게 두가지로 나눌 수 있다.

• Prediction: 주어진 Policy 하에서, 미래를 평가하는 것 = value function 을 잘 학습시키는 것
• Control: Policy를 최적화하는 것 = best policy를 찾는 것

 

• 그 외 용어

• Exploration: environment에 대한 새로운 정보를 발견하기 위해 이전에 해보지 않은 행동을 시도하는 것
• Exploitation: 이미 가지고 있는 정보들을 활용하여 reward를 최대화하는 것
  • RL 학습이 잘 이루어지려면 Exploration과 Exploitation 두 개념에 대한 균형이 중요하다

 

 

Markov Decision Process(MDP)

• 강화학습이 적용되는 문제 도메인은 모두 MDP(=완전히 관찰 가능한 환경)이다
• 강화학습은 MDP으로 모델링할 수 있는 환경에서 최적의 순차적 의사결정을 하는 것이다.

• MDP: RL에서의 environment를 표현 & environment가 모두 관측 가능한 상황을 말한다.
  • 모든 강화학습 문제는 MDP 형태로 만들 수 있다.

• Markov Process: n개의 State가 있고, 과거 경로에 관계없이 확률에 따라 State를 옮겨다니는 프로세스
  • State Transition Matrix: action없이 state를 확률에 따라 옮겨다님(Environment를 설명하기 위한 개념)
    • State S -> S'로 옮겨갈 확률 P_{ss'} = P[S_{t+1}=s' | S_t=s]일때, 모든 state의 확률을 나타내는 matrix

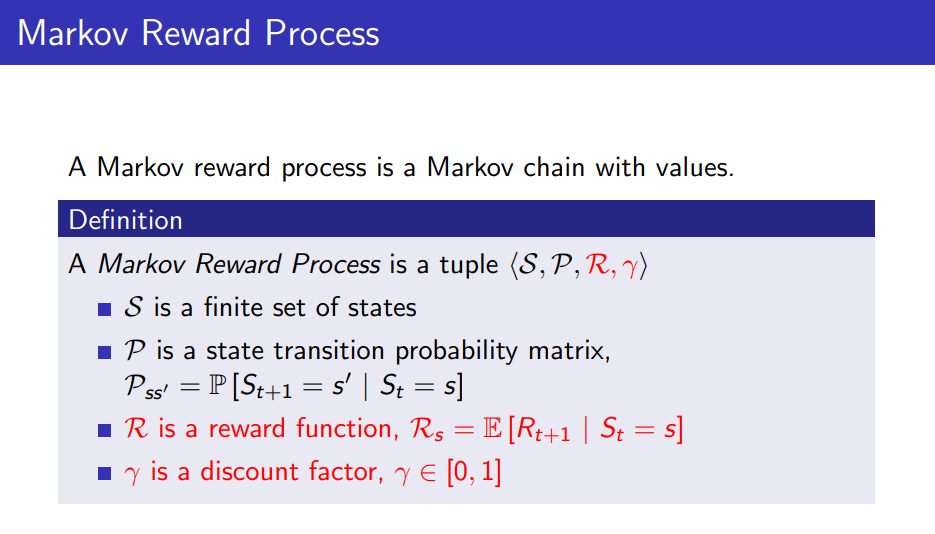
• Markov Reward Process: n개의 State가 있고, 과거 경로에 관계없이 확률에 따라 State를 옮겨다니는 프로세스로, State s일때의 reward는 R_s=E[R_{t+1} | S_t=s]이고 r(discount factor)는 0~1사이 값이다.
  • Return: 강화학습은 return을 maximize하는 것이다.
    • G_t = R_{t+1} + rR_{t+2} + ... = 미래의 리워드 합
  • Value Function: Return의 기대값 = State s에 왔을 때 G_t의 기대값
    • v(s) = E[G_t | S_t=s] = State s에서 시작한 여러 episode들의 평균
  • Bellman Equation: value function은 두가지 부분으로 나뉜다.
    • v(s) = E[G_t | S_t=s] = E[R_{t+1} + r(R_{t+2} + rR_{t+3} + ...) | S_t = s]
      
      • R_{t+1}: immediate reward
      • r(R_{t+2} + rR_{t+3} + ...): discounted value of successor state = r v(s_{t+1})
    • v(s) = R_s + r\sum_{s' from S} P_{ss'}v(s')
      • R_s: s일때의 reward
      • P_{ss'}: s->s'로 옮겨갈 확률
      • v(s'): s'일때 value function
    • 이를 행렬로 표현하면 V=(I-rP)^{-1}R이다. 즉, 주어져있는 값이므로 역행렬을 통해 한번에 계산이 가능하다.
      • computational complexity는 O(n^3)이므로 비싼 연산임
      • n이 작을 때는 한번에 계산 가능하지만, n이 클 때는 iterative(DP/Monte-Carlo Evaluation/Temporal Difference Learning)한 방법을 사용해야 한다.
• Markov Decision Process: n개의 State와 Action이 있고, 과거 경로에 관계없이 확률에 따라 State를 옮겨다니는 프로세스로, Action a를 하고 State s일때의 reward는 R_s^a=E[R_{t+1} | S_t=s, A_t=a]이고 r(discount factor)는 0~1사이 값이다.
  • State s에서 Action a를 하면 확률적으로 다른 State들에 도달하게 된다.
    • P_{ss'}^a = P[S_{t+1}=s' | S_t=s, A_t=a]: State s에서 Action a를 했을 때 State s'로 갈 확률
  • Policy: State s일때 Action a를 할 확률 = agent의 행동을 완전히 결정해줌
    • π(a|s) = P[A_t=a | S_t=s]
  • Value Function: 만약 agent의 policy가 고정되면 Markov process와 동일하다고 볼 수 있으며, reward도 마찬가지로 MRP로 볼 수 있음
    • State Value Function: State s에서 Policy π를 따랐을 때, episode들의 평균
      • v_π(s) = E_π[G_t | S_t=s]
    • Action Value Function: State s에서 Action a를 했을 때, 그 이후에는 Policy π를 따랐을 때의 기댓값
      • q_π(s,a) = E_π[G_t | S_t=s, A_t=a]
    • Bellaman Expectation Equation (= Prediction 문제): Bellman Eq.와 마찬가지로
      • v_π(s) = E_π[G_t | S_t=s] = E_π[R_{t+1} + rv_π(S_{t+1})| S_t=s] 
      • q_π(s,a) = E_π[R_{t+1} + rq_π(S_{t+1}, A_{t+1}) | S_t=s, A_t=a]
      • 위 두 식을 결합하면 v<->q로 표현할 수 있다.
        • v_π(s) = \sum_{a from Action} π(a|s) q_π(s,a)
        • q_π(s,a) = R_s^a + r\sum_{s' from State} P_{ss'}^a v_π(s')
        • v_π(s) = \sum_{a from Action} π(a|s) {R_s^a + r\sum_{s' from State} P_{ss'}^a v_π(s')}
      • MRP에서의 Bellman Eq.에 의해 행렬식으로 바꾸면 V_π = (I-rP_π)^{-1}R_π 로 구할 수 있다.
        • 마찬가지로 n이 커지면 구하기 어려우므로, q는 optimal value function을 이용하여 구한다.
  • Optimal Value Function
    • Optimal State Value Function: State s에서 어떤 policy를 따르든 간에, 그 중 가장 큰 value
    • Optimal Action Value Function: q*(s,a) = max_π(q_π(s,a))
    • Optimal Policy: 두 policy 중 더 나은 policy를 비교하기 위해서는 모든 State s에 대해 v_π(s) >= v_π'(s)가 성립하면 Policy π 가 Policy π' 보다 낫다고 할 수 있다.
      • Optimal Policy π*를 따르면 Optimal State Value Function v*(s)와 Optimal Action Value Function q*(s,a)를 구할 수 있다. 그리고 Optimal Policy는 q*(s,a)를 아는 순간 찾을 수 있다.
    • Bellman Optimality Equation (= Control 문제)
      • v*(s) = max_a(q*(s,a)): q*값들이 각 action마다 있을텐데, 그 중 max인 a를 선택하면 v*와 같다
      • q*(s,a) = R_s^a + r\sum_{s' from State} P_{ss'}^a v*(s')
      • 따라서 v*(s) = max_a(R_s^a + r\sum_{s' from State} P_{ss'}^a v*(s')): 이 식은 max 때문에 linear equation이 성립하지 않아 역행렬을 구하여 풀 수 없는 문제가 된다. 즉, 다양한 iterative solution method로 풀이를 해야한다.(value equation/policy equation/q-learning/sarsa)