이 문제에서 주의해야할 점은 아래 2가지이다.
- EOF 처리
- 최장부분증가수열을 빠르게 구하기
- 완전탐색 => O(2^N)
1차 시도 - `동적 계획법`을 사용하여 문제를 풀어보았다. 결과는 50%에서 시간초과.
=> O(N^2), N ≤ 100000이므로 1초안에 통과될 수 없다. 아마 10초정도 걸릴것임...ㅠㅠ
dp[n]: n번째 수를 마지막으로 하는 최장증가부분수열로 정의했다.
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNextInt()) {
int n = in.nextInt();
int[] stock = new int[n];
int[] dp = new int[n];
int max = 0;
for (int i = 0; i < n; i++) {
stock[i] = in.nextInt();
}
dp[0] = 1;
for (int i = 1; i < n; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++) {
if (stock[i] > stock[j]) {
dp[i] = Math.max(dp[j], dp[j] + 1);
}
}
max = Math.max(max, dp[i]);
}
System.out.println(max);
}
}
}
2차 시도 - N ≤ 100000이므로 1초안에 통과하려면 시간복잡도가 적어도 NlogN을 되어야 한다. => `이분탐색`을 이용한다
stock 수열을 처음부터 보면서
1. dp의 끝 값과 비교했을 때 마지막 값보다 큰 경우 dp의 마지막에 바로 삽입
2. dp의 끝 값과 비교했을 때 마지막 값보다 작거나 같은 경우 이분탐색을 이용하여 LIS를 유지하기 위한 위치에 수를 삽입하도록 한다.
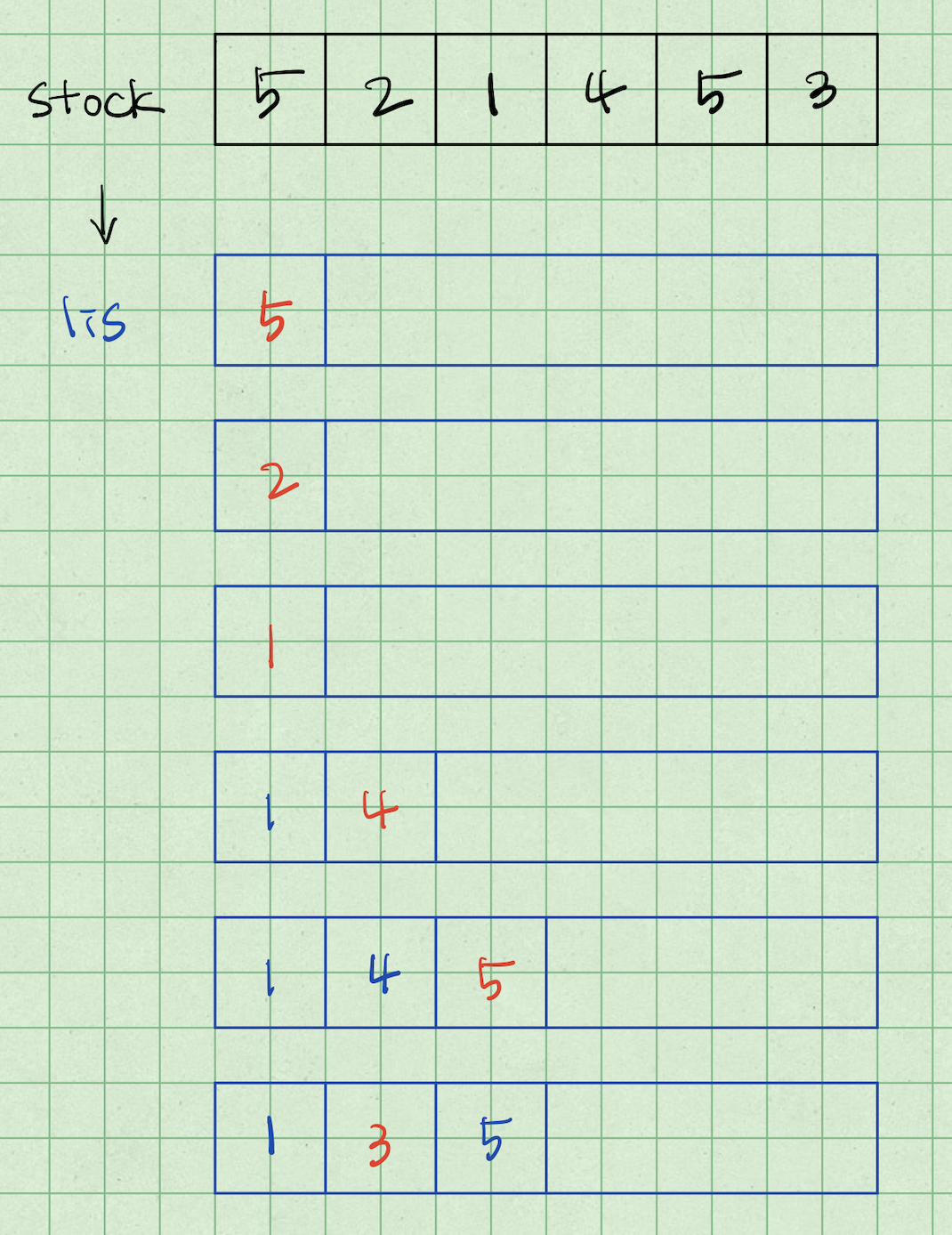
stock[0]을 dp 리스트에 넣는다.
stock[1]이 어디에 삽입될 수 있는지 인덱스를 이분탐색을 이용하여 구한다. (index=0)
stock[2]가 어디에 삽입될 수 있는지 인덱스를 이분탐색을 이용하여 구한다. (index=0)
stock[3]은 1보다 크므로 바로 삽입
stock[4]는 4보다 크므로 바로 삽입
stock[5]가 어디에 삽입될 수 있는지 인덱스를 이분탐색을 이용하여 구한다. (index=1)
예제에서 볼 수 있듯이 최종 dp 수열은 진짜 최장 증가 부분 수열을 이루는 요소와는 상관 없으며, lis의 길이만 연관이 있다는 점이 중요하다
위 알고리즘을 적용하여 코드를 짜 보면 아래와 같다.
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNextInt()) {
int n = in.nextInt();
int[] stock = new int[n];
int[] dp = new int[n];
for (int i = 0; i < n; i++) {
stock[i] = in.nextInt();
}
dp[0] = stock[0];
int lastIndex = 0;
for (int i = 1; i < n; i++) {
if (dp[lastIndex] < stock[i]) {
lastIndex++;
dp[lastIndex] = stock[i];
} else {
int index = findIndex(dp, stock[i], lastIndex);
dp[index] = stock[i];
}
}
System.out.println(lastIndex + 1);
}
}
public static int findIndex(int[] dp, int num, int lastIndex) {
int left = 0;
int right = lastIndex;
while (left < right) {
int mid = (left + right) / 2;
if (dp[mid] == num) {
return mid;
}
if (dp[mid] > num) {
right = mid;
} else {
left = mid + 1;
}
}
return right;
}
}
다른 방법으로는 `segment tree`를 사용하는 방법도 있다. segment tree를 사용하여 lis 길이를 구하는 방법은 아래와 같다.
1. 세그먼트 트리를 모두 0으로 초기화한다. , (stock[i], i) 객체를 만든 후 stock[i] 값에 대해 오름차순으로 정렬한다.
2. (stock[i], i)를 순회하면서 stock[i]에 대해 구간 [0, i]에서 최댓값을 구하고, 그 최대값+1을 세그먼트 트리의 인덱스 i인 리프 노드 값으로 업데이트한다. => i에 대해 구간 [0, i]에 지금까지 존재하는 LIS 길이+1 은 결국 stock[i]으로 끝나는 LIS길이와 같다.
3. 정렬된 객체를 순회하면서 LIS의 max 값을 찾는다.

가장 먼저 stock[i]=1인 i=2를 방문하게 된다.
먼저 구간 [0, 2]의 최댓값은 0이므로 1로 끝나는 LIS 길이는 1이고,
그 1 값을 인덱스 2에 업데이트 해 준다.
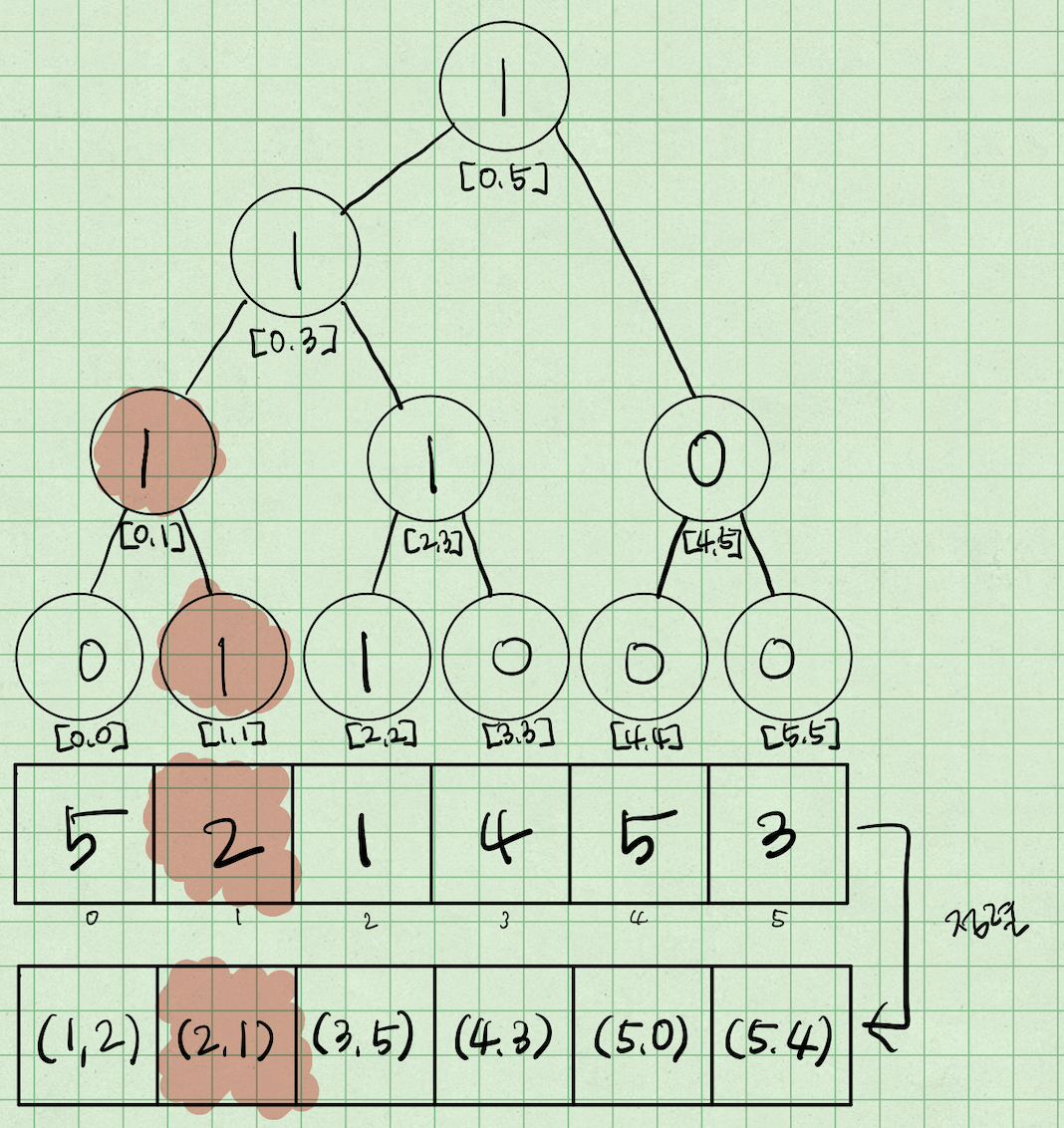
그 다음 stock[i]=2인 i=1를 방문하게 된다.
마찬가지로 [0, 1]의 최댓값은 0이므로 인덱스 1에 업데이트 해준다.
이때, 기존 LIS 결과가 증가하지는 않는다.
일단 이후 값이 언제 증가되는지 좀 더 보기로 하자.
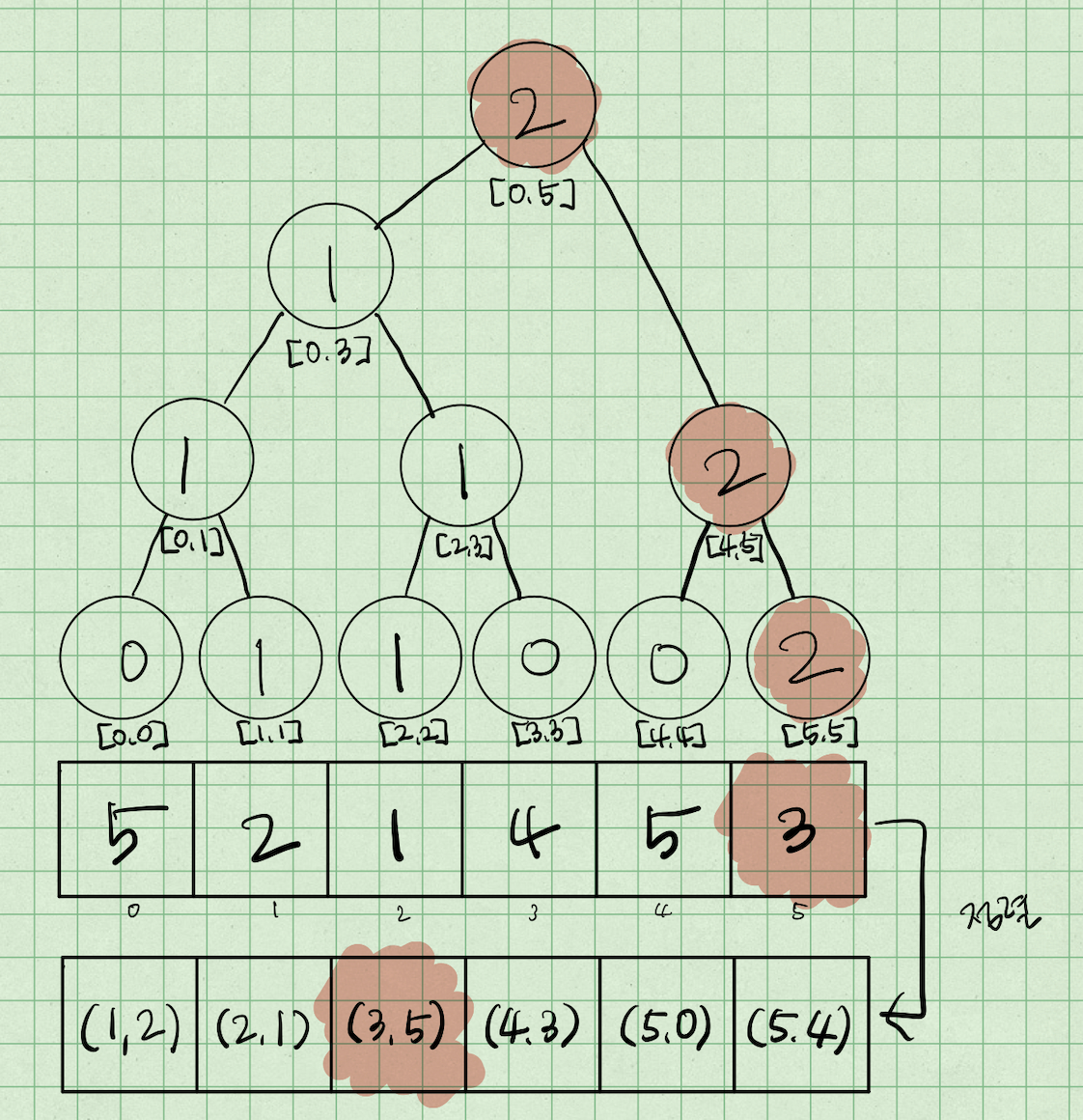
그 다음 stock[i]=3인 i=5를 방문하게 되는데,
[0, 5]의 최댓값은 1이므로 인덱스 5에 2를 업데이트 해준다.
즉, 새로 보는 원소가 기존의 LIS 길이를 증가시키려면
그 원소가 기존의 LIS보다 뒤에 나타나야 한다.
=> 이를 확인하는 것이 결국 구간 [0, i]의 최댓값을 보는 것이다.
이렇게 세그먼트 트리를 이용하여 stock[i]의 위치에 i번째 수를 마지막 원소로 가지는 lis의 길이를 업데이트함으로써 lis의 가장 긴 길이를 구할 수 있다.
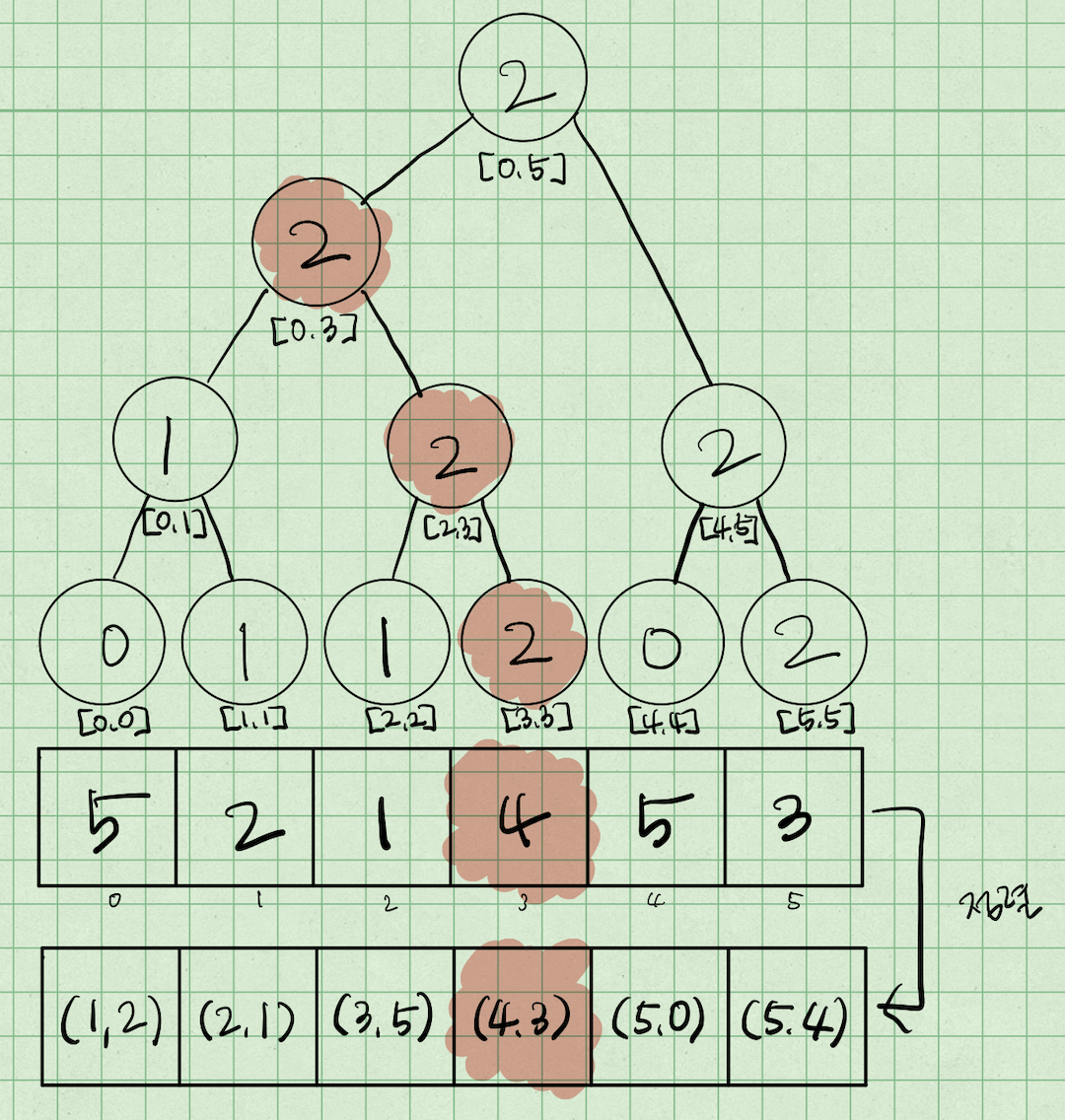
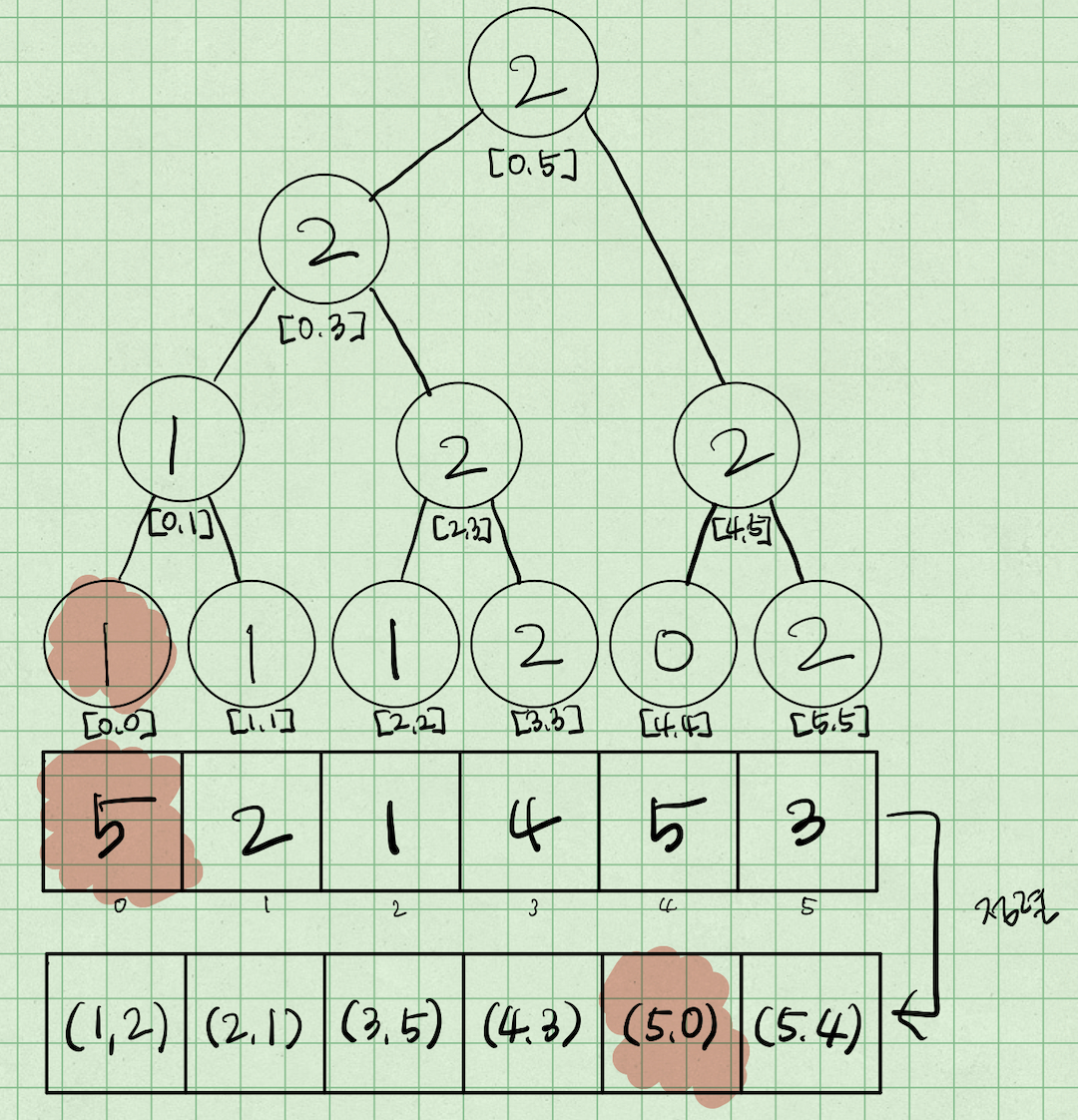
마찬가지로 stock[i]=4인 i=3를 방문하게 된다.
[0, 3]의 최댓값은 1이므로 인덱스 3에 1+1=2를 업데이트 해준다.
stock[i]=5인 i=0를 방문하게 된다.
[0, 0]의 최댓값은 0이므로 인덱스 0에 0+1=1을 업데이트 해준다.
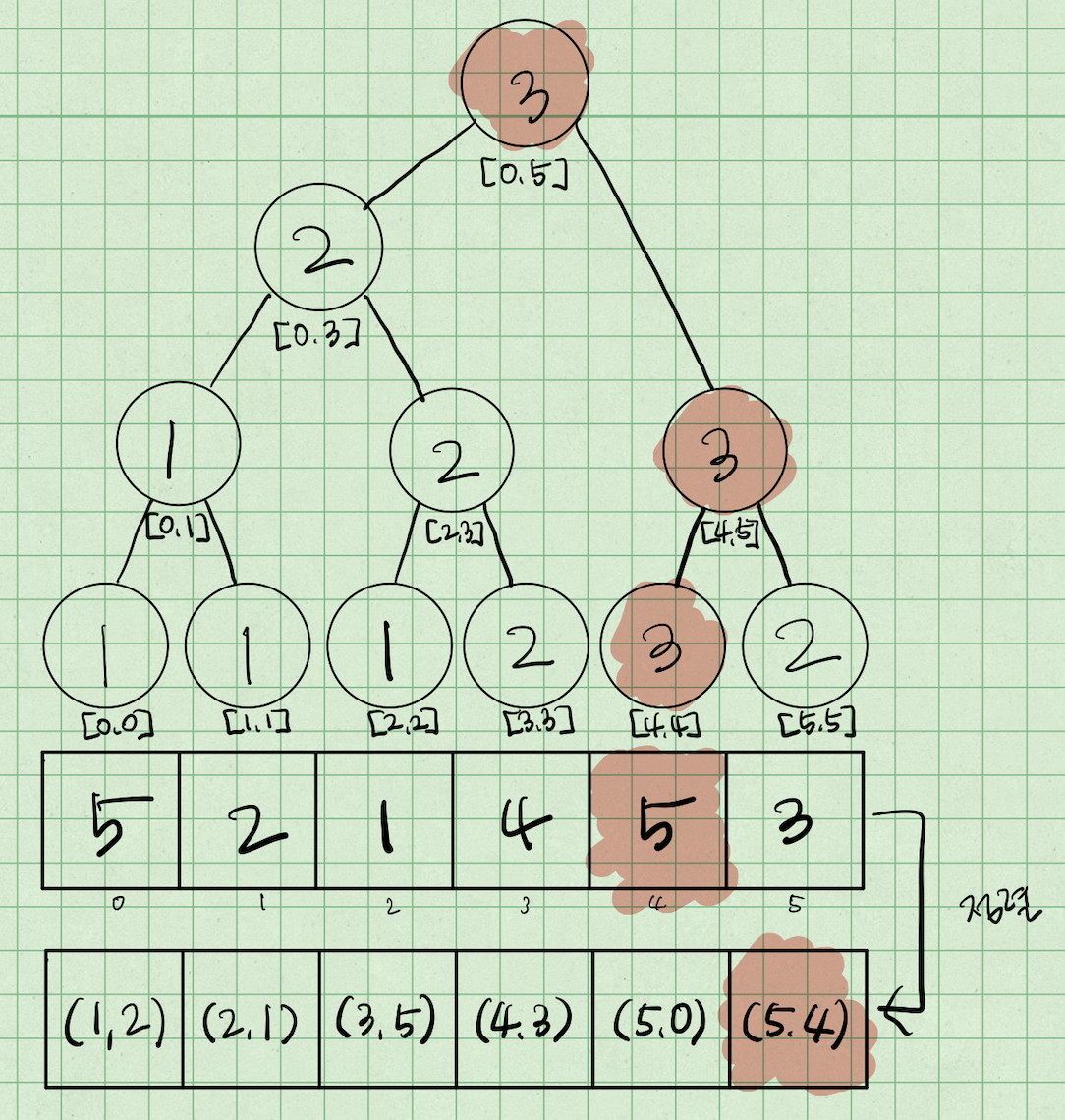
마지막으로 stock[i]=5인 i=4를 방문하게 된다.
[0, 4]의 최댓값은 2이므로 인덱스 4에 2+1=3을 업데이트 해준다
최종 구현을 직접 코드로는 안해봤지만... 나중에 업데이트 해 볼 생각히다
'알고리즘 공부 > boj' 카테고리의 다른 글
| boj 1949: 우수 마을 (0) | 2021.01.19 |
|---|---|
| boj 1981: 배열에서 이동 (0) | 2021.01.17 |
| boj 1091: 카드 섞기 (0) | 2021.01.11 |
| boj 1153: 네 개의 소수 (0) | 2021.01.10 |
| boj 17182: 우주 탐사선 (0) | 2021.01.10 |