설치 조건
- 기둥
- 바닥 위에 있거나 (y=0)
- 보의 한쪽 끝 부분 위에 있거나 다른 기둥 위에 있어야 한다 (아래와 이어져있다)
- 보
- 한쪽 끝 부분이 기둥 위에 있거나 또는 양쪽 끝 부분이 다른 보와 동시에 연결되어 있어야 한다. (왼쪽이나 오른쪽과 이어져있다)
- 기둥과 보는 길이가 1인 선분으로 표현된다.
예시
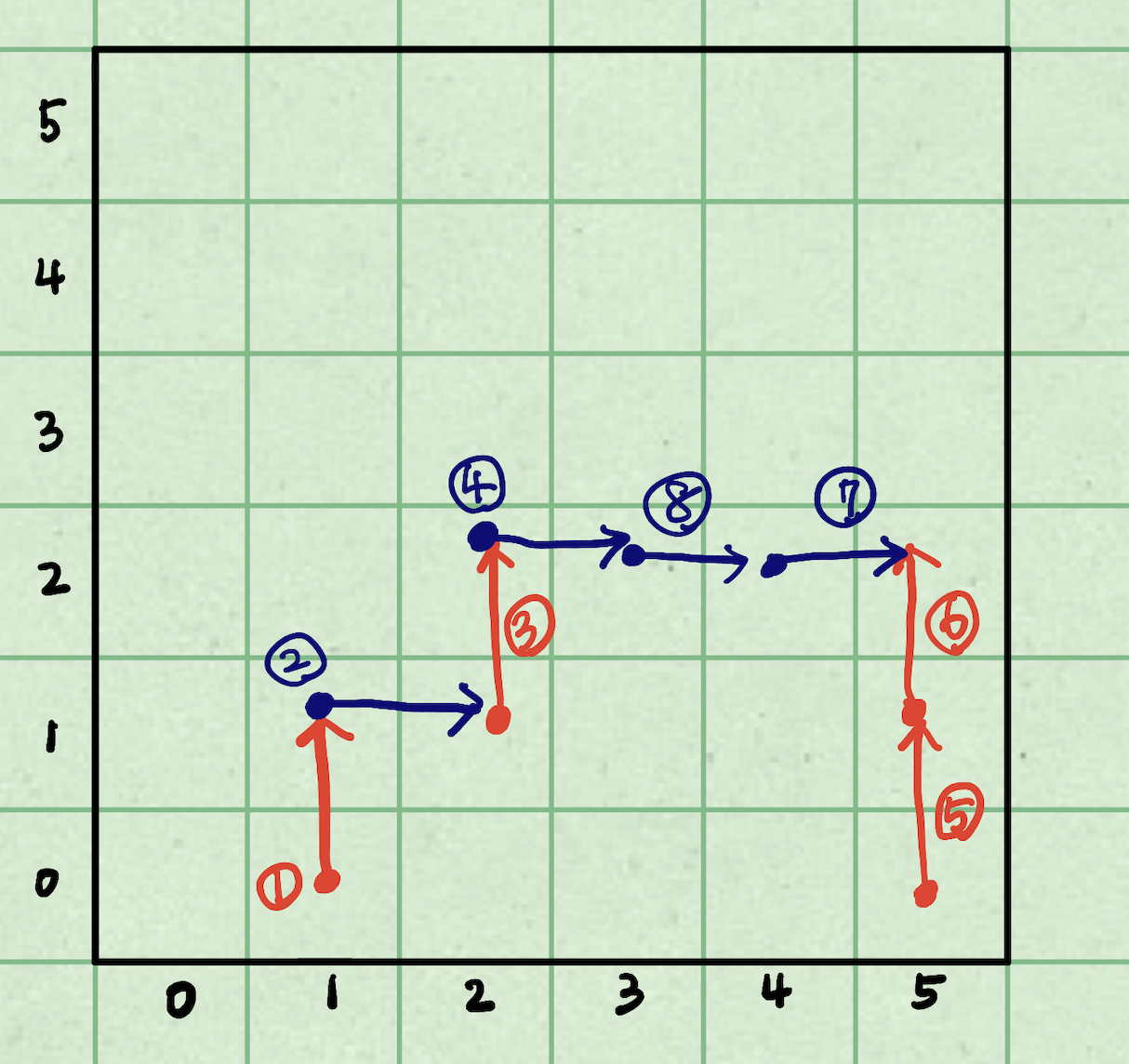
- (1, 0)에서 위쪽으로 기둥을 하나 설치 후, (1, 1)에서 오른쪽으로 보를 하나 만듭니다.
- (2, 1)에서 위쪽으로 기둥을 하나 설치 후, (2, 2)에서 오른쪽으로 보를 하나 만듭니다.
- (5, 0)에서 위쪽으로 기둥을 하나 설치 후, (5, 1)에서 위쪽으로 기둥을 하나 더 설치합니다.
- (4, 2)에서 오른쪽으로 보를 설치 후, (3, 2)에서 오른쪽으로 보를 설치합니다.
만약 (4, 2)에서 오른쪽으로 보를 먼저 설치하지 않고, (3, 2)에서 오른쪽으로 보를 설치하려 한다면 2번 규칙에 맞지 않으므로 설치가 되지 않습니다.
기둥과 보를 삭제하는 기능도 있는데 기둥과 보를 삭제한 후에 남은 기둥과 보들 또한 위 규칙을 만족해야 한다.
만약, 작업을 수행한 결과가 조건을 만족하지 않는다면 해당 작업은 무시된다.
어떻게 풀지 생각해 보다가 구조물을 추가할 수 있는지 여부를 보는 함수 addValid을 만들어 두고,
구조물을 제거할 때에는 구조물을 일단 제거한 뒤, 주위에 있는 기둥과 보를 다시 추가할 때 조건에 맞는지 여부를 addValid를 이용해서 보도록 했다.
이렇게 풀면 조건에 대해 세세하게 생각할 필요 없이 addValid 함수만 호출하면 되어서 쉽게 문제를 풀 수 있다.
import java.util.*;
class Solution {
public static int HORIZONTAL = 1;
public static int VERTICAL = 0;
public static int ADD = 1;
public static int DELETE = 0;
public int[][] solution(int n, int[][] build_frame) {
TreeSet<Structure> set = new TreeSet<Structure>();
for (int i = 0; i < build_frame.length; i++) {
int x = build_frame[i][0];
int y = build_frame[i][1];
boolean isVertical = build_frame[i][2] == VERTICAL ? true : false;
boolean isAdd = build_frame[i][3] == ADD ? true : false;
if (!isAdd) {
removeValid(x, y, isVertical, set);
} else {
addValid(x, y, isVertical, set);
}
}
int[][] answer = new int[set.size()][3];
int index = 0;
for (Structure s : set) {
answer[index][0] = s.x;
answer[index][1] = s.y;
answer[index][2] = s.structure;
index++;
}
return answer;
}
public void removeValid(int x, int y, boolean isVertical, TreeSet<Structure> set) {
if (isVertical) { // 기둥
if (set.contains(new Structure(x, y + 1, VERTICAL))) {
// 제거할 기둥 위에 기둥이 있는 경우
set.remove(new Structure(x, y, VERTICAL));
if (!addValid(x, y + 1, true, set)) {
set.add(new Structure(x, y, VERTICAL));
return;
}
}
if (set.contains(new Structure(x, y + 1, HORIZONTAL))) {
// 기둥 위에 오른쪽 보가 지탱이 안되는 경우
set.remove(new Structure(x, y, VERTICAL));
if (!addValid(x, y + 1, false, set)) {
set.add(new Structure(x, y, VERTICAL));
return;
}
}
if (set.contains(new Structure(x - 1, y + 1, HORIZONTAL))) {
// 기둥 위에 왼쪽 보가 지탱이 안되는 경우
set.remove(new Structure(x, y, VERTICAL));
if (!addValid(x - 1, y + 1, false, set)) {
set.add(new Structure(x, y, VERTICAL));
return;
}
}
set.remove(new Structure(x, y, VERTICAL));
return;
}
// 보
if (set.contains(new Structure(x, y, VERTICAL))) {
// 보 위에 기둥이 있는 경우
set.remove(new Structure(x, y, HORIZONTAL));
if (!addValid(x, y, true, set)) {
set.add(new Structure(x, y, HORIZONTAL));
return;
}
}
if (set.contains(new Structure(x + 1, y, VERTICAL))) {
// 보 오른쪽 위에 기둥이 있는 경우
set.remove(new Structure(x, y, HORIZONTAL));
if (!addValid(x + 1, y, true, set)) {
set.add(new Structure(x, y, HORIZONTAL));
return;
}
}
if (set.contains(new Structure(x + 1, y, HORIZONTAL))) {
// 오른쪽 보와 연결되어있는 보에 기둥이 없는 경우
set.remove(new Structure(x, y, HORIZONTAL));
if (!addValid(x + 1, y, false, set)) {
set.add(new Structure(x, y, HORIZONTAL));
return;
}
}
if (set.contains(new Structure(x - 1, y, HORIZONTAL))) {
// 왼쪽 보와 연결되어있는 보에 기둥이 없는 경우
set.remove(new Structure(x, y, HORIZONTAL));
if (!addValid(x - 1, y, false, set)) {
set.add(new Structure(x, y, HORIZONTAL));
return;
}
}
set.remove(new Structure(x, y, HORIZONTAL));
return;
}
public boolean addValid(int x, int y, boolean isVertical, TreeSet<Structure> set) {
if (isVertical) { // 기둥
if (y == 0) {
// 바닥 위에 있는 경우
set.add(new Structure(x, y, VERTICAL));
return true;
}
if (set.contains(new Structure(x - 1, y, HORIZONTAL)) || set.contains(new Structure(x, y, HORIZONTAL))) {
// 보의 한쪽 끝 부분 위에 있는 경우
set.add(new Structure(x, y, VERTICAL));
return true;
}
if (set.contains(new Structure(x, y - 1, VERTICAL))) {
// 다른 기둥 위에 있는 경우
set.add(new Structure(x, y, VERTICAL));
return true;
}
return false;
}
// 보
if (set.contains(new Structure(x + 1, y, HORIZONTAL)) && set.contains(new Structure(x - 1, y, HORIZONTAL))) {
// 양쪽 끝 부분이 다른 보와 동시에 연결
set.add(new Structure(x, y, HORIZONTAL));
return true;
}
if (set.contains(new Structure(x, y - 1, VERTICAL)) || set.contains(new Structure(x + 1, y - 1, VERTICAL))) {
// 한쪽 끝 부분이 기둥 위에 있는 경우
set.add(new Structure(x, y, HORIZONTAL));
return true;
}
return false;
}
}
class Structure implements Comparable<Structure> {
int x, y;
int structure;
public Structure(int x, int y, int structure) {
this.x = x;
this.y = y;
this.structure = structure;
}
@Override
public int compareTo(Structure o) {
if (x == o.x) {
if (y == o.y) {
return Integer.compare(structure, o.structure);
}
return Integer.compare(y, o.y);
}
return Integer.compare(x, o.x);
}
@Override
public boolean equals(Object o) {
if (this == o) {
return true;
}
if (!(o instanceof Structure)) {
return false;
}
Structure s = (Structure) o;
return x == s.x && y == s.y && structure == s.structure;
}
@Override
public int hashCode() {
return Objects.hash(x, y, structure);
}
@Override
public String toString() {
if (structure == 1) {
return "(" + x + ", " + y + ") 보";
}
return "(" + x + ", " + y + ") 기둥";
}
}'알고리즘 공부 > programmers' 카테고리의 다른 글
| Programmers 1843: 사칙연산 (0) | 2021.01.28 |
|---|---|
| Programmers 60062: 외벽 점검 (0) | 2021.01.27 |
| Programmers 1831: 4단 고음 (0) | 2021.01.24 |
| Programmers 42891: 무지의 먹방 라이브 (0) | 2021.01.24 |
| Programmers 67258: 보석 쇼핑 (0) | 2021.01.22 |